【問題】4人の死刑囚(ABCD)、自分の帽子の色が分かるのは誰?
自分の帽子の色が分かるのは、ABCDの一体誰でしょう?
★前提
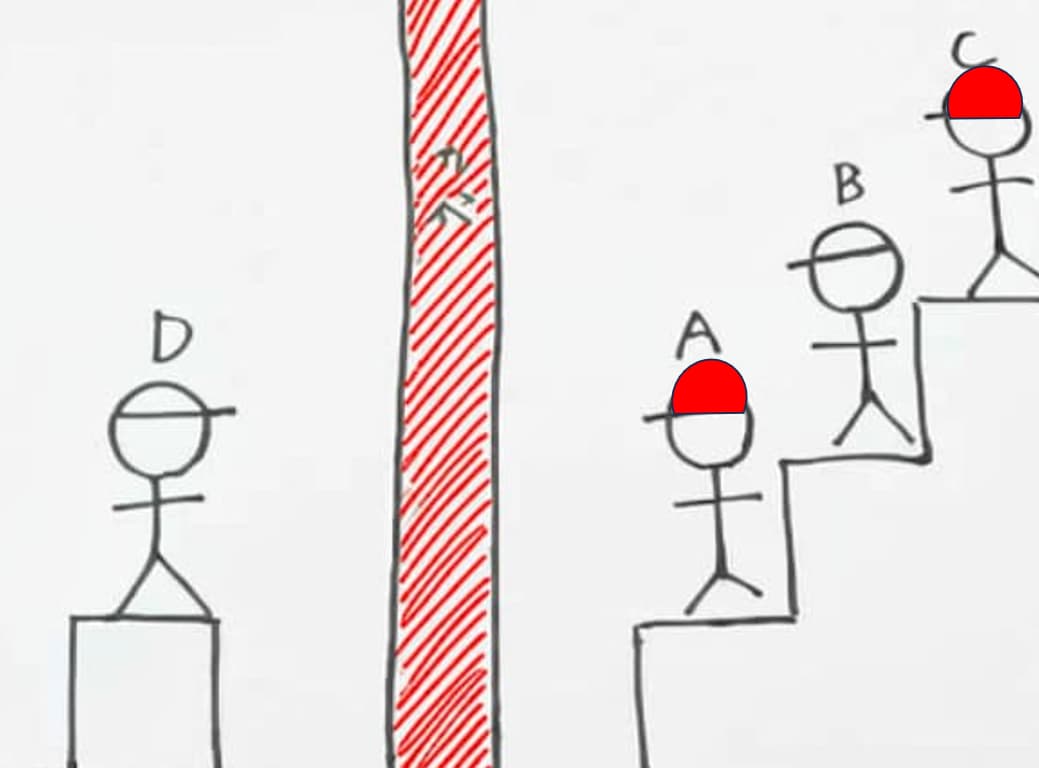
4人の死刑執行を待つ死刑囚(ABCD)は、赤or白のどちらかの帽子を被っていて、赤の帽子を被っているのはAとC、白の帽子を被っているのはBとD
前提条件の整理と解答と解説
前提条件の整理
状況: 4人の死刑囚(A, B, C, D)がいます。
帽子の種類と数: 赤色の帽子が2つ、白色の帽子が2つ。
各死刑囚の帽子の色:
A: 赤
B: 白
C: 赤
D: 白
視認範囲:
A: 誰の帽子も見えない。
B: Aの帽子が見える。
C: AとBの帽子が見える。
D: 誰の帽子も見えない。
ルール: 自分の帽子の色が分かったら、それを伝える。全員が非常に論理的思考力を持っている。
解答
この最新の前提条件の場合、自分の帽子の色が分かるのは、B です。
詳細な解説(論理のステップ)
このパズルでは、各人物が他の人物の行動(または沈黙)から、自分の情報を推測していく、という点が重要です。
ステップ1:DとAの視点
D: 誰の帽子も見えないため、自分の帽子の色を判断できません。
A: 誰の帽子も見えないため、自分の帽子の色を判断できません。
ステップ2:Cの沈黙
CはAの帽子(赤)とBの帽子(白)が見えています。
Cはすぐに自分の帽子の色を判断できません。なぜなら、自分(C)の帽子が赤でも白でも、A(赤)とB(白)が見えているという事実は変わらないからです。例えば、Cが赤だとしてもAとBは変わらず見え、Cが白だとしてもAとBは変わらず見えます。そのため、Cは沈黙します。
ステップ3:Bの視点(Cの沈黙がヒントになる)
BはAの帽子(赤)が見えています。
BはCが沈黙していることに気づきます。
Bは考えます。「CはAの帽子が見えている。もし私の帽子が赤だったとしたら、CはA(赤)と私(B:赤)という二つの赤い帽子を見ることになる。世の中には赤い帽子が2つしかないことを全員が知っているから、もしCの帽子が白であれば、Cは自分以外の2つが赤であることを見て『自分の帽子は白だ!』と即座に判断できるはずだ。」
「しかし、Cは沈黙している。これはCが自分の帽子の色を判断できていないことを意味する。Cが判断できていないのは、Cから見える帽子の組み合わせが、Cの帽子が赤である可能性を示唆しているからだ。」
「もし私(B)の帽子が赤だったら、CにはA(赤)と私(赤)の帽子が見え、Cが自分の帽子が白だと判断できたはずだ。しかし、Cは沈黙している。」
「Cが沈黙しているということは、Cが自分の帽子の色を即座に判断できない状況にあるということだ。それは、Cが私とAの帽子を見て、『両方赤』という状況ではない、ということだ。」
「Aの帽子は赤だと見えている。だから、私(B)の帽子は赤ではない。したがって、私の帽子は白だ。」
結論:
この最新の前提条件において、BがCの沈黙から自分の帽子の色を論理的に判断できます。
ネットの声

A「優しい世界・・・」

予備情報が一切ないので全員
「死刑囚は前しか見れない」
「喋ってはならない」
「自分の帽子を確認してはならない」
というルールがないので全員は帽子の色を確認して自分の色が解る。
「自分の帽子を確認してはならない」ならABCが、相談して解る。

自分で確認すれば全員分かるし、全員白で全員赤
リバーシブルになっていて、両サイド引っ張ってつばを上に立たせればウルトラマンになれる

ちょっと上を見れば自分の帽子のツバが見えると思う。だから全員自分の帽子の色が分かる!!!

Bじゃない?
Cは2人の帽子の色が見えてるけど壁の向こうの人の色がわからないから答えない
Cが答えないことによってBはAとは違う色ということがわかる

この「4人の死刑囚ハットパズル」のポイントは、「Aが答えられなかった」ことによって、Bが自分の帽子の色を論理的に導き出すところにあります。
パズルの前提
•死刑囚はA・B・C・Dの4人。
•それぞれ赤か白の帽子を被っている。
•実際にはAとCが赤、BとDが白。
•下図のように、AはBとCを見られる、BはCだけを見られる、Cは前が見えず、Dは壁で仕切られており誰も見えない。
•ただし帽子の配分数(赤が2つ、白が2つ)などはわかっているとする場合が多い。
(C:赤) ──最上段
↑ (B:白) ──中段
↑ (A:赤) ──下段
~~~壁~~~
(D:白)
なぜBが自分の帽子の色を言い当てられるのか
1.Aの視点
•AはBとCの帽子を同時に見ている(B:白、C:赤)。
•もしBが「赤」を被っていたら、Aの目の前には「B:赤、C:赤」の“赤×2”が見えるはずです。
•Aは「赤帽子は全部で2個」という情報を持っていると仮定すると、「自分(A)が赤か白か」は、B・Cがもし両方赤なら自分は白しか残らない……というふうに論理的に分かるはず。
•ところがAは即答できず「自分の帽子の色を特定できない」状態にある。
2.Bの視点
•BはC(赤)を見ている。
•Aが答えられなかった理由をBは考える。
•もし自分(B)が「赤」なら、Aから見ると「B:赤、C:赤」になるため、Aはすぐに「自分は白だ」とわかるはず。
•しかしAは答えられなかった。つまりAの目の前に「赤×2」は存在しない。
•よってBは「自分は赤ではあり得ない → 白である」ことを確信できる。
3.CやDには何もわからない
•Cは前を見ても誰もいないので情報が少なく、自分の色を特定できない。
•Dは壁があり、さらに周囲の反応も見えないため論理を組み立てる材料がない。
結論
よって、自分の帽子の色を「確実」に言い当てることができるのはB です。